Alles so schön bunt hier!

Es wird mal wieder Zeit für ein kleines bisschen zweckbefreite Spielerei hier. Hatten wir ja auch schon länger nicht mehr. Der nichtige Anlass ist eine Diskussion über die farbigen Schlieren auf einem Ölfilm auf nasser Strasse. Die Erklärung dafür kennt man vielleicht noch aus der Schule - es ist die Interferenz. Das an der Grenzfläche von Luft zu Öl reflektierte Licht überlagert sich, sofern die Dicke des Ölfilms gering genug ist, mit dem von der Grenzfläche Öl-Wasser reflektiertem Licht in einer festen Phasenbeziehung. Addiert man die beiden reflektierten Wellen, dann verstärken oder schwächen sie sich gegenseitig, je nach Wellenlänge des Lichts, Dicke des Ölfilms und Einfallswinkel des Lichts. Kennt man die Brechungsindizes von Luft, Öl und Wasser, dann kann man auch ausrechnen, bei welchen Wellenlängen sich die beiden reflektierten Wellen maximal verstärken oder abschwächen. Ich hab das mal in einer kleinen Skizze zusammengefasst:

Durch das Verstärken und Abschwächen bei verschiedenen Wellenlängen kommt ein Farbeffekt zustande, der mit der Dicke des Ölfilms variiert und so Farbschlieren auf einem Ölfleck hervorbringt.
An dieser Stelle hören die Erklärungen von der Wikipedia bis zum Physikbuch normalerweise auf. Nur bleibt doch noch die Frage, welche Farben man denn nun genau sehen sollte bei einer bestimmten Dicke des Ölfilms, und ob das auch die Farben sind, die man tatsächlich sieht? Also, ziehen wir es durch! Bringen wir es zum Ende! Bestimmen wir die genaue Farbabfolge, die man auf einem Ölfilm auf nasser Strasse sehen sollte!

Dazu brachen wir drei Dinge. Erst einmal müssen wir wissen, welcher Anteil des einfallenden Lichts bei einer bestimmten Wellenlänge genau reflektiert wird. Dazu müssen wir die reflektierten Wellen mit der richtigen Phasenverschiebung addieren. Allerdings müssen wir auch wissen, welcher Anteil der Welle an einer Grenzfläche reflektiert wird, und welcher gebrochen wird und in die folgende Schicht weiterläuft. Kann man noch hinbekommen, braucht man die Wikipediaartikel zur Interferenz und den Fresnelschen Formeln zu… Genau genommen müssten wir allerdings nicht nur zwei Strahlen betrachten, denn die Aufspaltung zwischen reflektiertem Anteil und gebrochenen Anteil findet ja immer wieder statt. Etwa so:

Gut, in der Praxis erhalten wir sicher eine sehr gute Näherung, wenn wir nur die ersten zwei austretenden Strahlen betrachten. Die Amplitude der austretenden Welle wird mit jeder weiteren Reflexion und Brechung stark abnehmen und der wesentliche Beitrag kommt durch die Überlagerung des direkt reflektierten Anteils und des ersten wieder austretenden Anteils zustande. Trotzdem. Die Überlagerung von nur zwei Wellen, mal echt jetzt - das ist doch was für Pussies! Wer Interferenz mit zwei Strahlen macht, der ruft auch bei Papierstau nach dem Admin und hält Tofu für ein menschliches Nahrungsmittel! Wir berechnen den reflektierten Anteil des einfallenden Lichts aus der Überlagerung aller (im Prinzip unendlich vieler) Strahlen richtig und benutzen dazu die Transfermatrix-Methode. Darauf, wie die funktioniert, gehen wir hier aber nicht ein [1]. Was sonst noch nötig ist, das sind die wellenlängenabhängigen Brechungsindizes für Luft, Wasser und das Öl. Sowas kann man sich gut hier besorgen. Für das Öl nehmen wir mal die Werte für Benzol. Davon sollte zwar (hoffentlich) nicht allzu viel im Öl drin sein, mit seinem Brechungsindex von um die 1,5 ist es aber ziemlich typisch für Öliges und was Besseres habe ich nicht gefunden. Wird's schon tun. Jetzt können wir den reflektierten Anteil des Lichts für jede Wellenlänge des Lichts und für verschiedene Dicken des Öl- oder genauer, Benzolfilms, auf Wasser ausrechnen. Die Ergebnisse sind hier mal in einer Animation zusammengefasst:

Der Wellenlängenbereich auf der x-Achse entspricht in etwa dem Bereich des sichtbaren Lichts, der violette Teil des Spektrums ist am linken Ende der Achse, der Rote am rechten Ende. Auf der y-Achse ist der reflektierte Anteil des auf den Benzolfilm auftreffenden Lichts in Prozent aufgetragen. Der Lichteinfall ist hier (und der Einfachheit halber im ganzen Rest dieses Textes immer) senkrecht.
Man erkennt, wie sich mit ansteigender Dicke des Benzolfilms ein immer dichteres Interferenzmuster aus Minima und Maxima im reflektierten Licht aufbaut und wie es sich mit der Wellenlänge verändert. Es kommt übrigens nie, wie in vielen einfachen Beispielrechnungen üblich, zu einer völligen Auslöschung des reflektierten Lichts im Falle maximal destruktiver Interferenz. Das liegt daran, daß die Amplituden der einzelnen reflektierten Wellen unterschiedlich sind (sie sind durch die Unterschiede in den Brechungsindizes der verschiedenen Schichten festgelegt) und sie sich nie komplett gegenseitig aufheben können. So bleibt auch im Minimum immer etwa 2% des Lichts übrig.

So weit, so gut. Die Erste der drei Zutaten haben wir damit. Wir können für jede Wellenlänge und für jede Schichtdicke den Anteil des reflektierten Lichts ausrechnen. Aber die Farbe, die man beim Blick auf die Benzolschicht auf dem Wasser sieht, hängt nicht nur davon ab, welcher Anteil des einfallenden Lichts bei welcher Wellenlänge reflektiert wird. Sondern auch, wieviel Licht bei welcher Wellenlänge überhaupt auf die Oberfläche auftrifft. Mithin also von der Beleuchtung. Damit können wir es uns ruhig einfach machen. Es gibt viele standardisierte Beleuchtungen. Für solche Standardisierungen ist die Internationale Beleuchtungskommission CIE zuständig. Das klingt vielleicht erst einmal ein bisschen merkwürdig, aber wenn man sich überlegt, welche Bedeutung Farben und Beleuchtungen in allen Bereichen des menschlichen Lebens haben, dann ist es eigentlich nicht mehr verwunderlich, dass es auch jemanden gibt, der für sowas Industrienormen macht. Eine häufig verwendete (und letztlich hier besonders einfache zu handhabende) Standardbeleuchtung ist das Spektrum mit dem poetischen Namen D65. Das ist ein Beleuchtungsspektrum, das repräsentativ für das diffuse Tageslicht um die Mittagszeit in Mitteleuropa ist. Man kann es sich bei der CIE herunter laden, so sieht es aus:

Das nehmen wir, und fertig ist Teil zwei. Wenn wir dieses Beleuchtungsspektrum mit einer berechneten Reflexionskurve für eine gewünschte Schichtdicke multiplizieren, dann bekommen wir die tatsächlich bei jeder Wellenlänge von der Oberfläche ausgehende Lichtmenge heraus.

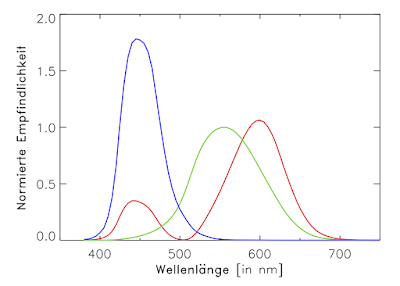
Jetzt fehlt noch der dritte und letzte Teil. Die Farbe, die wir beim Blick auf den Benzolfilm wahrnehmen, hängt nicht nur vom reflektierten Anteil des einfallenden Lichts und der Beleuchtung ab, sondern auch noch von der wellenlängenabhängigen Lichtempfindlichkeit des menschlichen Auges. Das klingt kompliziert, aber auch hier können wir einfach bei Standardisierungen bleiben. Denn die CIE normiert nicht nur Beleuchtungen, sondern auch die menschliche Wahrnehmung.
Die Netzhaut des Auges enthält drei verschiedene Arten von farbempfindlichen Sinneszellen mit maximalen Empfindlichkeiten bei verschiedenen Wellenlängen. Aus diesen drei Reizen wird die menschliche Farbwahrnehmung zusammengesetzt. Die normierten Empfindlichkeiten dieser drei Zellenarten in Abhängigkeit von der Wellenlänge gibt's auch auch den CIE-Seiten. Sie bilden den "CIE kolorimetrischen Standardbeobachter" von 1931 und sehen so aus:

Wenn wir jede dieser drei Empfindlichkeitskurven mit dem Ergebnis unserer vorherigen Schritte (der bei jeder Wellenlänge von der Oberfläche ausgehende Lichtmenge) multiplizieren und das Ergebnis über die Wellenlängenachse integrieren, dann bekommen wir drei Zahlen heraus, eine für jeden Typ von Farbwahrnehmungszellen in der Netzhaut. Diese drei Zahlen heissen "Tristimulus", die Stimulation der drei Sinneszellen, und sind die Farbe, die wir sehen. Machen wir die ganze Rechnung mal für eine Benzolschicht mit einer Dicke von 0.35 Mikrometern, dann ist das Ergebnis die drei Zahlen 442,6, 335,4 und 629.2.
Noch nicht sehr beeindruckend. Was uns für eine Interpretation fehlt, ist das psychologische Element bei der Sache. Welchen Farbeindruck habe ich denn, wenn meine farbempfindlichen Sehzellen Stimulationswerte von 442,6, 335,4 und 629,2 erleben? Praktischerweise ist auch das wieder in Industrienormen geregelt. So gibt es für verschiedene Farbräume Umrechnungsvorschriften, mit deren Hilfe man vom Tristimulus zu einer Farbe kommt. Wir können z.B. den Standard-RGB-Farbraum, sRGB, nehmen. Das ist der Farbraum, den Computermonitore gerne benutzten. In diesem Farbraum wird jede Farbe durch die Mischung von drei Grundfarben erzeugt, Rot, Grün und Blau (Jaaa, der Name "RGB" ist kein Zufall!). Die Intensität der jeder dieser drei Grundfarben in der Mischung wird durch eine 8-bit-Zahl beschrieben, d.h. einer Zahl im Wertebereich von 0 bis 255. Die Umrechungsvorschrift vom Tristimulus in die drei Intensitätswerte im sRGB-Frabraum können wir uns z.B. bei der Wikipedia besorgen. Für den Beispielfall der Benzolschicht mit 0,35 Mikrometern Dicke liefern die Tristimuluswerte die Intensitätswerte von 68, 40 und 69.
Gut, immer noch nicht so wahnsinnig beeindruckend. Aber jetzt können wir einfach dem Computer sagen, benutze den sRGB-Farbraum und setzte die Intensitätswerte des roten, grünen und blauen Farbkanals auf 68, 40 und 69. Dann taucht eine Farbe auf dem Bildschirm auf. Und unter allen Farben, die der Bildschirm (im sRGB-Farbraum) darstellen kann, ist dies dann die Farbe, die dem Farbeindruck beim Betrachten eines Benzolfilms von 0,35 Mikrometern Dicke auf Wasser unter typischer Tageslichtbeleuchtung am nächsten kommt. So:

Also ein dunkles Violett. Damit sind wir durch. Alles, was zu tun bleibt, ist die Farbe für alle möglichen Schichtdicken zu berechnen und in einen Farbbalken einzutragen. So sehen die Farbmuster eines Benzolfilms auf Wasser in Abhängigkeit von der Filmdicke aus:

Die Farben wirken alle recht dunkel. Das liegt daran, daß in der Berechnung nur Licht von oben einging und alles Licht, das ins Wasser hinein gelangt, auf Nimmerwiedersehen darin verschwindet. Es ist also das Ergebnis für einen perfekt schwarzen Hintergrund. Um die Farben deutlicher zu sehen, können  wir sie ein bisschen aufhellen. Auch wenn das eigentlich nicht so ganz koscher ist, wie sehen die Farben dann deutlicher:

Und diese Farben können wir jetzt mit den Farben auf einem schillernden Ölfleck vergleichen. Hier:

(via HyperPhysics)

Wenn wir annehmen, daß der Ölfilm am Rande des Flecks am dünnsten ist und zur Mitte hin dicker wird, dann können wir die Farbabfolge von außen nach innen mit der Farbfolge im Farbbalken von links nach rechts vergleichen: Erst kommt ein hellgrauer Farbton, der geht ins Beige über, dann Violett, das erst ins Dunkelblaue und dann in ein immer helleres Blau übergeht. Dann kommt so eine Art Senfton, der ins Violette und von da wieder ins Blaue geht. Dann kommt wieder Grün, Violett und wieder Grün und dann etwas Grau. Die berechneten Farbtöne und deren Abfolge passt schon ziemlich gut mit dem Aussehen des Flecks zusammen!

Na gut, eine so große Leistung ist es im Grunde nicht, die Farbabfolge richtig hin zu bekommen. Denn die ist eigentlich immer dieselbe. Ändern sie Brechungsindizes etwas, dann ändert sich die Intensität der Farben und die Zuordnung zur Dicke der Schicht. Die Farbtöne selbst und deren Reihenfolge wird aber  kaum verändert. Die Form der Interferenzmuster bleibt halt immer dieselbe, nur ihre Intensität und Lage  ändern sich. So bekommt man ganz ähnliche Ergebnisse, wenn man den Farbbalken für eine Seifenblase ausrechnet, oder genauer gesagt, für einen dünnen Wasserfilm. Beim Durchschauen gegen diffuses Tageslicht erhält man so ganz zarte Farben:

Im reflektierten Licht vor einem schwarzen Hintergrund sieht man sie deutlich, es gibt wieder den Farbverlauf wie beim Öl:

Oder nehmen wir mal eine dünne Siliciumnitridschicht auf Silicium. Die Farben beim Betrachten dieser Schicht sind in ihrer Abfolge wieder dieselben:

In diesem Fall sorgt der hohe Brechungsindex von Siliciumnitrid für kräftige Farben und einen schnellen Wechsel.

Das Beispiel einer Siliciumnitridschicht auf Silicium ist auch gar nicht so abwegig, wie es auf den ersten Blick vielleicht scheint. Man kann durchaus den Wunsch verspüren, Licht in Silicium hinein zu bekommen. Zum Beispiel, wenn das Silicium eine Solarzelle ist. Leider ist Silicium aber relativ stark reflektierend, und so würde ein nennenswerter Anteil des Lichts von der Oberfläche einer Solarzelle einfach wieder nutzlos reflektiert werden, und nicht in sie eindringen, wo fleissige kleine Wichtel dann Ökoelektronen aus dem Licht formen und in die Steckdosen werfen. Um die Leistung einer Solarzelle zu erhöhen, wird sie also mit einer Antireflexionsbeschichtung versehen. Die soll, wie der Name ja nahelegt, die Reflexion von Licht minimieren. Wenn man eine solche Schicht aufbringen will, dann sollte deren Brechungsindex zwischen dem der Luft und des Siliciums liegen, am Besten bei der Wurzel aus dem Brechungsindex von Silicium (sowas verrät einem z.B. die Wikipedia). Der ist ungefähr 4, also sollte man als Beschichtungsmaterial etwas mit einem Brechungsindex um die 2 suchen. Siliciumnitrid hat einen solchen Brechungsindex und ist außerdem noch relativ einfach aufzubringen. Daher eine solche Beschichtung. Die optimale Dicke einer solchen Schicht richtet sich nach der Wellenlänge, für die man die Reflexionsunterdrückung optimieren will. Ideal ist die diese Wellenlänge, geteilt durch 4 mal den Brechungsindex der Schicht (sagt auch Wikipedia). Eine gute Wahl wäre eine Optimierung für eine Wellenlänge von 550 bis 600 Nanometern, dort ist die Sonnenstrahlung auf der Erdoberfläche am stärksten. Daraus folgt eine Schichtdicke von 70 ins 75 Nanometern (d.h. 0.07 bis 0.075 Mikrometern). Guckt man im letzten Farbbalken nach, dann sieht man, daß eine solche Oberfläche tiefblau aussieht. Und damit ergibt sich auch, warum die gemeine Feld-, Wald- und Wiesensolarzelle aus Silicium so schön blau ist, obwohl sie doch aus grauem Silicium gemacht ist.

Will man nun wirklich einmal andere Farbverläufe sehen, dann muß man zu ganz anderen Materialien gehen. Metalle zum Beispiel. Sagen wir mal, Gold. Wir können uns auch mal den Farbbalken für eine dünne Goldschicht auf Glas ansehen. Bei der Draufsicht sieht das so aus:

Da Gold wie alle Metalle Licht sehr stark absorbiert, muß die Schicht sehr dünn sein, damit überhaupt noch was durch kommt. Der Wertebereich der x-Achse ist hier deutlich kleiner als in allen vorherigen Balken. Sehr schnell hat die Schicht nur noch die Goldfarbe. Bei sehr geringen Dicken aber ist die Farbe irgendwo im rötlich-braunen Bereich. Wir können noch mal nachsehen, wie das im Durchgucken im Gegenlicht aussieht:

Wenn die Schicht von außen einfach nur golden aussieht, ist sie von innen pechschwarz. Man blickt einfach nur auf ein Stück Gold, durchscheinen tut da nichts mehr. Solange aber noch was durchscheint, sieht das goldbeschichtete Glas von außen bräunlich aus, von innen aber grün.

Gold- oder anderweitig metallbeschichtete Gläser benutzt man nicht nur in Blogs, sondern auch in der wirklichen Welt, z.B. als thermisches Isolierglas, denn so beschichtete Scheiben sind für Infrorotstrahlung sehr undurchlässig. Und der rotbraune Farbton kommt einem vielleicht von irgendwelchen Hochhausglasfassaden bekannt vor. Der Palast der Republik hatte auch metallbeschichtete, rötlich-braune Fenster. Von innen tendieren Glasscheiben mit einer einfachen Goldbeschichtung aber zum Grünstich beim Rausgucken.

So, das reicht für heute mal. Von Ölflecken über Seifenblasen und Solarzellen zu Thermofenstern, mehr passt in einen Blogpost nicht mehr rein. Wer bis hierhin durchgehalten hat, darf sich zur Belohnung auf meine Kosten ein Gratis-Youtube-Video seiner Wahl anschauen. Wer nicht bis hierhin gekommen ist, sogar ein Kostenpflichtiges!

[1] Ja, das ist jetzt schon ein bisschen frech. Aber leider lässt sie sich nicht in drei Sätzen erklären. Eine rudimentäre Erklärung findet der interessierte Leser in der englischsprachigen Wikipedia. Wer es aber wirklich genau wissen will, der kommt, fürchte ich, nicht umhin, zu einem der einschlägigen Lehrbücher zum Thema zu greifen -  z.B. Knittel: Optics of Thin Films (pdf, siehe Kapitel 2.5).
Das Praktische an dieser Methode ist, daß sie es erlaubt, den reflektierten Anteil und den durchgehenden Anteil des Lichts für beliebige Einfallswinkel und für eine beliebige Anzahl von ebenen Schichten mit beliebigen Brechungsindizes und bei Bedarf auch mit Absorption von Licht in Schichten sehr einfach und schnell auszurechnen. Dazu folgt sie nicht den verschiedenen Strahlen, sondern nutzt geschickt die Randbedingungen aus, die die Maxwellgleichungen dem elektrischen Feld der Lichtwellen an den Grenzflächen aufzwingen. Wer Freude an eleganten mathematischen Lösungen für kompliziert aussehende Probleme hat (oder zumindest ein extravagantes Verständnis des Begriffs "Freude"), der wird daran eine Menge Spass haben!