Keine Sorge, allzu schlimm wird das gar nicht. Physikkenntnisse benötigen wir quasi gar keine. Was es braucht, sind solide Kenntnisse der Schulmathematik, aber wer hat die schon? Aber wir haben ja die Wikipedia im Rücken, um sie notfalls ein bisschen aufzufrischen. Und wir brauchen ein paar grundlegende Programmierkenntnisse, aber das sollte ja im 21. Jahrhundert zur guten Allgemeinbildung gehören? Wir wollen es auch nicht unnötig kompliziert machen und nehmen eine weit verbreitete Feld-, Wald- und Wiesenprogrammiersprache, Java etwa. Und wir halten den Code auch so schlicht wie möglich. Das sollte mir leicht fallen, denn ich bin auch nicht gerade ein Experte in Java. Aber da zeige ich einfach mal Mut zur Häßlichkeit. Ich meine, Hauptsache, am Ende funktioniert's! Und wer mit Java Probleme hat, der kann sich ja mal bei der Wikipedia in den Artikeln Java (Programmiersprache) und Java-Syntax ein bisschen einlesen...
So, dann wollen wir mal. Und daß jetzt niemand auch nur daran denke, wegzuklicken oder gleich zum Ende zu springen! Heute geben wir dem kleinen Nerd in uns mal ordentlich Zucker, und keiner verlässt den Raum!
Das Problem an sich
Wenn wir die Positionen der Planeten im Sonnensystem angeben wollen, dann haben wir eigentlich drei Teilprobleme zu lösen: Erstens müssen wir wissen, die die Umlaufbahnen der Planeten aussehen. Also, wirklich genau aussehen, nicht nur so ein allgemeines Blahblah. Dann müssen wir irgendwie ausrechnen können, wo ein Planet zu einer vorgegebenen Zeit gerade auf seiner Umlaufbahn ist. Und dann müssen wir als drittes den Ort auf seiner Umlaufbahn irgendwie in ein allgemeines, von seiner Bahn unabhängiges Koordinatensystem umrechnen. Denn nur in so einem allgemeinen Koordinatensystem für alle Planeten können wir ja die Positionen der Planeten zueinander, und damit ihre Abstände bestimmen.Zur Lösung der ersten beiden Teilprobleme brauchen wir nichts weiter als die drei Keplerschen Gesetze, an die man sich vielleicht noch dunkel aus der Schule erinnert. Die müssen wir allerdings ordentlich mathematisch ausschlachten. Das dritte Teilproblem ist eigentlich nur ein bisschen Vektorrechnung. Fangen wir also erst einmal bei den Keplerschen Gesetzen an!
Die Keplerschen Gesetze
Die Wikipedia sagt uns, daß die Bewegung der Planeten im Sonnensystem einigermaßen gut durch die Keplerschen Gesetze beschrieben wird: "sie [sind] eine gute Näherung für die tatsächlich in einem Sonnensystem durchlaufenen Planetenbahnen." Nehmen wir also einfach mal an, daß sich die Planeten gemäß den drei Keplerschen Gesetzen bewegen. Das erste der drei Gesetze lautet laut Wikipedia:"Die Planeten bewegen sich auf elliptischen Bahnen, in deren einem Brennpunkt die Sonne steht."Nehmen wir das mal beim Wort. Um die Umlaufbahn eines Planeten um die Sonne anzugeben, müssen wir also eine Ellipse angeben. Was brauchen wir, um eine Ellipse im Raum anzugeben? Der von den Keplerschen Gesetzten aus verlinkte Artikel Bahnelemente hilft weiter. Wir brauchen zwei Größen, die die Form der Ellipse bestimmen: eine dieser Größen legt die Ausmaße der Ellipse fest, die andere, wie langgestreckt sie ist. Wir lesen, daß wir hier die große Halbachse für die Größe der Ellipse und die Exzentrizität für ihre Form nehmen können.
Jetzt brauchen wir noch drei Winkel, die angeben, wie die Ellipse im Raum orientiert ist. Der erste dieser Winkel ist die Inklination. Dieser Winkel gibt an, um wieviel die Ebene, in der die Ellipse liegt, gegenüber einer Referenzebene geneigt ist. Als Referenzebene wollen wir hier die Ebene der Erdbahn, die Ebene der Ekliptik, nehmen. Wikipedia meint, das sei durchaus üblich. Die beiden anderen notwenigen Winkel müssen jetzt noch angeben, wie die Ebene, in der die Ellipse liegt, bezüglich einer festgelegten Richtung gedreht ist, und wie die Ellipse innerhalb dieser Ebene gedreht ist. Als festgelegte Richtung in der Bezugsebene, also in der Ebene der Erdbahn, nehmen wir die Richtung des Frühlingspunkts. Das ist die Richtung, in der die Sonne von der Erde aus gesehen am Frühlingsanfang steht. Für die beiden uns noch fehlenden Winkel nehmen wir hier die Winkel mit den schönen Namen Argument des Knotens und Argument der Periapsis. Haben wir diese insgesamt fünf Größen, dann ist die Umlaufbahn eines Planeten im Raum eindeutig festgelegt.
Nur eines fehlt uns, nämlich ein "Startpunkt". Wir müssen noch für einen Zeitpunkt wissen, wo der Planet gerade auf seiner Umlaufbahn ist, dann können wir ausrechnen, wo er zu jedem beliebigen anderen Zeitpunkt ist. Dabei hilft uns dann das zweite Keplersche Gesetz. Als Angabe für den Ort des Planeten auf seiner Ellipse zu einem bestimmten Zeitpunkt nehmen wir die sogenannte Mittlere Anomalie. "Anomalie" ist hier einfach nur ein schönes Wort für Winkel in der Ebene der Bahnellipse. Jetzt haben wir sechs Größen, die wir für einen Planeten kennen müssen, um seine Bewegung komplett beschreiben und seine Position für einen beliebigen Zeitpunkt bestimmen zu können. Das ist alles recht abstrakt, aber der Wikipedia-Artikel Keplerbahn bietet immerhin eine Graphik zur Illustration.
Woher sollen wir diese sechs Größen, die Bahnelemente, bekommen? Aus der Wikipedia natürlich. Die englischsprachige Wikipedia gibt die sechs Größen in den Artikeln zu den einzelnen Planeten in der Tabelle rechts oben unter dem Stichpunkt "Orbital characteristics" an.
Dann wollen wir auch schon mal ans Programmieren gehen. Wir machen uns ein Java-Projekt namens "WikiEphem" und darin ein erstes Paket "solarSystemObject". Als erstes können wir uns eine Aufzählungsklasse erstellen, die die acht Planeten mit ihren Bahnelementen aus der Wikipedia vordefiniert. Das könnte dann etwa so aussehen:
package solarSystemObject;
public enum Planet {
// Die Zahlenwerte für die Bahnelemente der einzelnen Planeten aus der Wikipedia:
MERCURY(0.387098, 0.205630, 7.005, 48.331, 29.124, 174.796),
VENUS(0.723327, 0.006756, 3.39458, 76.678, 55.186, 50.115),
EARTH(1.00000261, 0.01671123, 0.0, 348.73936, 114.20783, 357.51716),
MARS(1.523679, 0.093315, 1.850, 49.562, 286.537, 19.3564),
JUPITER(5.204267, 0.048775, 1.305, 100.492, 275.066, 18.818),
SATURN(9.58201720, 0.055723219, 2.485240, 113.642811, 336.013862, 320.346750),
URANUS(19.22941195, 0.044405586, 0.772556, 73.989821, 96.541318, 142.955717),
NEPTUNE(30.10366151, 0.011214269, 1.767975, 131.794310, 265.646853, 267.767281);
// Die Bahnelemente der Planeten (für den 1.1.2000, 12:00h, d.h.J2000):
private double a; // Große Halbachse (in AE)
private double e; // Exzentrizität (einheitenlos)
private double i; // Inklination (in Grad)
private double OMEGA; // Argument des aufsteigenden Knotens (in Grad)
private double omega; // Argument des Perihels (in Grad)
private double M; // Mittlere Anomalie (in Grad)
/*
* Konstruktor, der die Planeten "erzeugt":
*/
private Planet(double a,double e,double i,double OMEGA,double omega,double M){
this.a = a;
this.e = e;
this.i = i;
this.OMEGA = OMEGA;
this.omega = omega;
this.M = M;
}
// Die "getters", mit die Bahnelemente abgefragt werden können.
// (Winkel lassen wir uns gleich ins Bogenmaß umrechnen)
public double getA(){
return this.a;
}
public double getE(){
return this.e;
}
public double getI(){
return Math.toRadians(this.i);
}
public double getOMEGA(){
return Math.toRadians(this.OMEGA);
}
public double getOmega(){
return Math.toRadians(this.omega);
}
public double getM(){
return Math.toRadians(this.M);
}
}
Fertig. Jetzt der nächste Schritt. Wie können wir die Position des Planeten auf seiner Umlaufzeit aussrechnen, wenn wir seine Bahnelemente haben? Nehmen wir das zweite Keplersche Gesetz her:
"Ein von der Sonne zum Planeten gezogener „Fahrstrahl“ überstreicht in gleichen Zeiten gleich große Flächen."Die Idee ist einfach: Dieses Gesetz sagt irgendwie etwas über die Geschwindigkeit des Planeten entlang seiner Umlaufbahn aus. Wenn wir einen Ort auf der Umlaufbahn zu einer bestimmten Zeit kennen, und wir etwas über die Geschwindigkeit wissen, dann sollten wir doch irgendwie die Orte zu anderen Zeiten ausrechnen können. Um eine solche Rechnung in der Praxis durchzuführen, benötigt man einige Hilfskonstruktionen, die noch auf Kepler persönlich zurück gehen. Die Wikipedia verrät sie uns im Artikel Kepler-Gleichung. Um die beachtliche Länge dieses Posts nicht noch weiter zu steigern, verweisen wir hier einfach nur auf den Artikel und benutzen seine Aussagen direkt ohne weitere Erläuterungen. Im Zweifel sollte man einfach den Artikel lesen. Das Fazit ist dieses:
Wir können also die mittlere Anomalie M eines Planeten leicht berechnen, wenn wir seine Umlaufzeit U und den Zeitpunkt t0 kennen, an dem er den sonnennächsten Punkt durchläuft.
M = 2 π (t-t0) / U (1)Wenn wir die exzentrische Anomalie E kennen, können wir mit der Exzentrizität e (einer der sechs Bahnelemente) die wahre Anomalie T leicht ausrechnen:
cos T = [cos E - e] / [1 - e cos E] (2)Den Zeitpunkt, an dem der Planet seinen sonnennächsten Punkt durchläuft, bekommen wir aus der sechsten von uns ausgesuchten Bahnelemente, der mittleren Anomalie zu einem festen Zeitpunkt. Die Umlaufzeit U bekommen wir einfach aus dem dritten Keplerschen Gesetz:
"Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen (Kuben) der großen Bahnhalbachsen."Dieses Gesetz ist enorm praktisch! Denn es erlaubt es uns, die großen Halbachsen, einer der von uns gewählten sechs Bahngrößen, und die Umlaufzeiten mit den Werten für die Erde zu verknüpfen. Die Umlaufzeit der Erde kennen wir leicht, das ist (in etwa) ein Jahr. Und die große Halbachse der Erdbahn soll einfach den Wert 1 haben. Die Einheit nennen wir dann Astronomische Einheit, und es muß uns zur Berechnung der Planetenpositionen gar nicht interessieren, wie groß dieser Wert in absoluten Einheiten, etwa in Kilometern, ist. Natürlich kennt man den Wert der Astronomischen Einheit heute in Kilometern. Aber lange Zeit war er nicht bekannt, und man konnte dennoch alle Positionen im Sonnensystem maßstäblich richtig berechnen!
So. Alles, was uns jetzt also noch fehlt, ist der Zusammenhang zwischen der mittleren Anomalie M und der exzentrischen Anomalie E, dann könnten wir uns zu jedem Zeitpunkt die wahre Anomalie eines Planeten, und damit seine Position auf seiner Umlaufbahn ausrechnen. Dieser Zusammenhang steht natürlich auch im Wikipedia-Artikel zur Kepler-Gleichung, denn er ist ja gerade die Kepler-Gleichung:
E - e sin E = M (3)Diese Gleichung, die E und M verknüpft, ist für unser Schulwissen ein bisschen eklig. Es ist eine implizite Gleichung. In ihr tritt die Größe E direkt und als Argument einer Funktion, in diesem Fall der Sinusfunktion, auf und wir können sie nicht einfach so durch Umstellen nach E auflösen. Aber praktischerweise verrät uns die Wikipedia auch, wie wir diese Gleichung für ein gegebenes M näherungsweise für E lösen können: Wir ziehen auf beiden Seiten der letzten Gleichung M ab. Dann suchen wir dasjenige E, das eine Nullstelle einer Funktion f (E) ist. Und für das Suchen von Nullstellen einer Funktion gibt es sehr einfache und gute numerische Verfahren. Wikipedia legt uns hier gleich eines der einfachsten Verfahren nahe, das Newton-Verfahren. In unserem Fall lautet das dann:
En+1 = En + f (En) / f ' (En) (4)Die Ableitung f ' (E) ist leicht berechnet: f ' (E) = 1 - e cos(E). Wir müssen also mit einem Startwert E0 anfangen und solange den neuen Werte En+1 nach der obigen Gleichung aus dem alten Wert En ausrechnen, bis der zugehörige Wert f (En+1) so nahe an der Null ist, daß wir meinen, gut damit Leben zu können. Dann haben wir mit dem letzten Wert En einen guten Näherungswert für die exzentrische Anomalie E bestimmt. Und welchen Startwert E0 nehmen wir? Die englischsprachige Wikipedia empfiehlt uns an dieser Stelle den Startwert E0 = M für Umlaufbahnen mit nicht zu großer Exzentrizität e und den Startwert E0 = π für Umlaufbahnen mit großer Exzentrizität, z.B. Kometen. Die Planeten haben alle eine recht kleine Exzentrizität, also folgen wir der Wikipedia-Empfehlung und nehmen den Startwert E0 = M. Schreiben wir uns also einen kleinen Java-Code, der die Kepler-Gleichung für uns löst mit diesem Näherungsverfahren löst, und schon wir haben den Kern des Problems geknackt!
Aber halt, ein kleines technisches Problem bleibt erst noch zu beseitigen! Wir werden ja gleich Zeitdifferenzen (t - t0) für unsere Rechnungen benötigen. Im Alltag gibt man Zeiten aber üblicher- und bequemerweise als Kalenderdaten und Uhrzeiten an. Kalenderdaten und Uhrzeiten sind aber sehr unbequem, um Zeitdifferenzen auszurechnen. Ich meine, wieviel Zeit (in Sekunden, in Stunden, Tagen, was auch immer) liegt denn z.B. zwischen dem 2. September 1999, 21:21, und dem 19. Februar 2017, 06:19? Eben. Wir brauchen eine Methode, um Zeitdifferenzen bequem ausrechnen zu können. Dafür gibt es auch ein Hilfsmittel, auch in der Wikipedia, das Julianische Datum. Dabei handelt es sich einfach um eine fortlaufende Zählung von Tagen, angefangen am 1. Januar 4713 v. Chr. um 12 Uhr mittags. Kennt man die Julianische Daten, also einfach zwei Zahlen (mit Nachkommastellen), zu zwei Kalenderdaten, dann ist der Zeitunterschied zwischen den beiden Kalenderdaten einfach die Differenz der Julianischen Daten, gerechnet in Tagen. Sowas ist bequem, sowas wollen wir. Und wir müssen auch gar nicht lange rumüberlegen, denn die Wikipedia gibt im Artikel gleich eine ausgiebig kommentierte Anleitung, wie Kalenderdaten in Julianische Daten umzurechnen sind. Folgen wir einfach den dort angegebenen Schritten! Wir machen uns also noch ein Java-Paket mit Hilfmitteln, "Tools", und erzeugen uns darin eine Klasse mit Julianischen Daten. Das sieht dann z.B. so aus:
public class JulianDate {
private double jd;
private double year;
private double month;
private double day;
private double hour;
private double minute;
/*
* Dieser Konstruktor erzeugt ein Julianisches Datum aus einem Kalendertag.
* Die kleinste verwendete Zeiteinheit ist die Minute, kleinere Zeiteinheiten
* müssen als Bruchteile einer Minute angegeben werden.
*/
public JulianDate(int day, int month, int year, int hour, double minute){
this.year = (double) year;
this.month = (double) month;
this.day = (double) day;
this.hour = (double) hour;
this.minute = minute;
this.jd = getJulianDate();
}
/*
* Dieser Konstruktor erzeugt ein Julianisches Datum nur aus dem
* Julianischen Tag. Das ist praktisch, wenn man ab einem Stichtag
* nachher Zeitserien durchrechnen will.
*/
public JulianDate(double jdn){
this.jd = jdn;
}
/*
* Die Methode, die zu einem bestimmten Kalenderdatum das Julianische Datum ausrechnet
*/
private double getJulianDate(){
double Y = this.year;
double M = this.month;
if (this.month < 2){
Y--;
M += 12.0;
}
double D = this.day;
double H = this.hour/24.0 + Math.floor(this.minute)/1440.0 +
(this.minute - Math.floor(this.minute))/86400.0;
double A;
double B=0;
// Wenn "true", benutze Gregorianischen Kalender (default),
// ansonsten benutze Julianischen:
boolean Gregorian = true;
// Verwende sicher Julianischen Kalender:
if (this.year < 1582 || this.year == 1582 && this.month < 10){
Gregorian = false;
}
// Der kompliziertere Fall, daß die Kalenderreform im Monat liegt:
if (this.year == 1582 && this.month == 10){
if (this.day <= 4){
Gregorian = false;
} else {
if (this.day > 4 && this.day < 15){
System.out.println(
"Fehler: Dieses Datum existiert nicht
(Gregorianische Kalenderreform)!");
}
}
}
if (Gregorian){
A = Math.floor(Y/100.0);
B = 2.0 - A + Math.floor(A/4.0);
} else {
B = 0.0;
}
return Math.floor(365.25*(Y+4716.0)) + Math.floor(30.6001*(M+1.0)) +
D + H + B - 1524.5;
}
// Gibt das Julianische Datum aus
public double getJD()
return this.jd;
}
}
So, haben wir das auch. Dann schreiben wir uns doch auch gleich mal eine Klasse, die die Keplersche Umlaufbahn eines Planeten enthält. Also etwa sowas:
public class KeplerianOrbit {
// Die Bezugsgrößen:
private double AEARTH = 1.00000261; // Die große Halbachse der Erdbahn (in AE)
private double YEAR = 365.2563604167;// Umlaufzeit der Erde in Tagen (ein Jahr)
private JulianDate EPOCH = new JulianDate(1,1,2000,12,0.0); // Der Referenzzeitpunkt
// Eine Umlaufbahn hat sechs Bahnelemente:
private double a; // Große Halbachse (in AE)
private double e; // Exzentrizität (einheitenlos)
private double i; // Inklination (im Bogenmaß, d.h. rad)
private double OMEGA; // Argument des aufsteigenden Knotens (in rad)
private double omega; // Argument des Perihels (in rad)
private double M; // Mittlere Anomalie (in rad)
/*
* Ein Konstruktor, der einfach die Bahnelemente eines Planeten übernimmt:
*/
public KeplerianOrbit(Planet planet){
this.a = planet.getA();
this.e = planet.getE();
this.i = planet.getI();
this.OMEGA = planet.getOMEGA();
this.omega = planet.getOmega();
this.M = planet.getM();
}}
In diese Klasse packen wir uns jetzt alles rein, was wir nach den oben gesagten Schritten zur Berechnung der Position eines Planeten brauchen. Also als erstes mal die Umlaufperiode nach dem dritten Keplerschen Gesetz:
// Berechnet die Umlaufzeit (in Tagen) aus dem 3. Keplerschen Gesetz
private double getPeriod(){
return Math.sqrt(YEAR*YEAR * Math.pow(this.a / AEARTH), 3);
}
// Rechnet die mittere Anomalie zu einem Zeitpunkt t aus
private double getMeanAnomaly(JulianDate t){
return (2.0*Math.PI * (t.getJD() - EPOCH.getJD()) / getPeriod() + this.M)
% (2.0*Math.PI);
}
So, jetzt kommt die Berechnung der exzentrischen Anomalie mit dem Näherungsverfahren aus Gleichung (4) dran:
// Berechnet die exzentriche Anomalie zu einer Zeit t mittels Newton-Raphson-Naeherung
private double getEccentricAnomaly(JulianDate t){
// Berechne die augenblickliche mittere Anomalie:
double meanAnomaly = getMeanAnomaly(t);
// Setze den Startwert von E auf M
double Eold = meanAnomaly;
// Initialisieren
double Enew = 0.0;
// Die gewünschte Genauigkeit, bricht ab, wenn die Änderung unter diesen Wert fällt:
double acc = 1.0E-8;
// Initialisieren
double change = 1.0;
// Starte die Iteration. (Schleche Konvergenz ist nicht vorgesehen...)
while (change > acc){
// Berechne den Funktionswert am alten Wert von E:
double f = Eold - this.e * Math.sin(Eold) - meanAnomaly;
// Berechne die Ableitung am alten Wert von E:
double fd = 1.0 - this.e * Math.cos(Eold);
// Berechne den neuen Wert von E:
Enew = Eold - f/fd;
// Gucke mal, um wieviel sich der neue Wert noch vom alten unterscheidet:
change = Math.abs(Enew/Eold - 1.0);
// Setze den alten Wert von E auf den neuen Wert
// und wiederhole die Iteration wenn nötig:
Eold = Enew;
}
return Enew;
}
Schon durch! Kennen wir jetzt die exzentrische Anomalie, können wir die wahre Anomalie T ausrechnen. Der Wikipedia-Artikel Kepler-Gleichung gibt den Zusammenhang mit der exzentrischen Anomalie an:
tan( T/2 ) = √[ (1 + e) / (1 - e) ] * tan( E/2 ) (5)Wir werden aber auch gleich gewarnt, daß die Umkehrung der Tangensfunktion beim Auflösen dieser Gleichung nach T eine Fallunterscheidung erforderlich macht. Der Artikel True anomaly in der englischen Wikipedia erklärt diese Fallunterscheidung noch ein bisschen genauer. Der Java-Code sieht trotzdem einfach aus:
// Berechnet die wahre Anomalie zu einer gegeben exzentrischen Anomalie
private double getTrueAnomaly(double E){
return 2.0 * Math.atan2(Math.sqrt(1.0+this.e)*Math.sin(E/2.0),
Math.sqrt(1.0-this.e)*Math.cos(E/2.0));
}
r = a [ 1 - e cos( E ) ] (6)Das ist einfach:
// Berechnet den Abstand von der Sonne zu einer gegebenen exzentrischen Anomalie
private double getRadialPosition(double E){
return this.a * (1.0 - this.e * Math.cos(E));
}
Transformationen
So, jetzt haben wir alles, um den Ort eines Planeten in seiner Umlaufbahn auszurechnen, die wahre Anomalie T, also den Winkel zwischen seiner Position und dem sonnennächsten Punkt seiner Bahn und seinen Abstand von der Sonne, r. Dies sind Koordinaten in Polarkoordinaten, die wir nur noch in Koordinaten in einem kartesischen Koordinatensystem im Raum umrechnen müssen. Am besten, wir verwenden gleich dreidimensionale Vektoren um die Position des Planeten anzugeben, auch schon bei den Polarkoordinaten in der Bahnebene. Berechnen wir uns also erst einmal die Position in Polarkoordinaten an einem Julianischen Datum t:
/*
* Berechnet den Ort des Planeten zu einer gegebenen Zeit t in Kugelkoordinaten.
* Die Koordinaten sind r - der Abstand von der Sonne, der Winkel T (die wahre
* Anomalie) gemessen vom sonnennächsten Punkt der Bahn) und pi/2 (die Bewegung
* des Planeten erfolgt in einer Ebene, d.h. in zwei Dimensionen, und zweite,
* konstante Winkel wird konventionell "von oben in die Ebene" gemessen.)
*/
public Vector getPositionInOrbit(JulianDate t){
double E = getEccentricAnomaly(t); // Berechne die exzentrische Anomalie
return new Vector(getRadialPosition(E),getTrueAnomaly(E),Math.PI/2.0);
}
public class Vector {
// Die drei Komponenten x, y, z eines Vektors in drei Dimensionen
private double x;
private double y;
private double z;
// Erzeugt einen Vektor aus drei Zahlen für die drei Komponenten
public Vector(double theX, double theY, double theZ){
this.x = theX;
this.y = theY;
this.z = theZ;
}
// "Getters":
public double getX(){
return this.x;
}
public double getY(){
return this.y;
}
public double getZ(){
return this.z;
}
// Berechnet den Differenzvektor zwischen den Vektoren a und b
public static Vector subtract(Vector a, Vector b){
return new Vector(a.getX() - b.getX(), a.getY() - b.getY(), a.getZ() - b.getZ());
}
// Berechnet die Länge eines Vektors a
public static double norm(Vector a){
return Math.sqrt(a.getX()*a.getX() + a.getY()*a.getY() + a.getZ()*a.getZ());
}
}
Das ist schon alles in Sachen Vektoren. Aber wir werden in unserem lineare Algebra-Paket auch noch Matrizen brauchen. Denn jetzt müssen wir ja von unseren Polarkoordinaten in der Bahnebene zu kartesischen Koordinaten umrechnen. Und wie geht das? Na, erst mal machen wir uns kartesische Koordinaten in einem Koordinatensystem in der Bahnebene. Die Umrechung ist einfach, die finden wir in der Wikipedia z.B. beim Artikel Kugelkoordinaten, der dreidimensionalen Variante unserer Polarkoordinaten. Machen wir uns schnell noch eine Java-Klasse "Koordinatentransformationen", z.B. im Paket "Tools", und rechnen um:
public class CoordinateTransformations {
// Transformiert einen Vektor von Kugelkoordinaten zu Kartesischen Koordinaten
public static Vector sphericalToCartesian(Vector vector){
double X = vector.getX() * Math.sin(vector.getZ()) * Math.cos(vector.getY());
double Y = vector.getX() * Math.sin(vector.getZ()) * Math.sin(vector.getY());
double Z = vector.getX() * Math.cos(vector.getZ());
return new Vector(X,Y,Z);
}
}
Und wie führen wir die Drehungen praktisch aus? Wie gesagt, wie brauchen Matrizen. Denn die Wikipedia verrät, daß Drehungen durch Drehmatrizen beschrieben werden. Der gedrehte Vektor ergibt sich durch die Multiplikation des ungedrehten Vektors mit einer Drehmatrix. Die Drehmatrix hat eine recht einfache Form, sie hängt von der Drehachse und dem Drehwinkel ab.
Jetzt haben wir zwei Optionen. Entweder, wir nehmen und Papier und Bleistift und rechnen einmal allgemein aus, wie wir den Ortsvektor unseres Planeten durch Drehung umrechnen müssen. Dazu müssen wir drei Matrizenmultiplikationen durchführen. Das ist mühsam und stupide, gibt aber eine effizientere Berechnung mit dem Computer. Oder aber, wie schreiben uns einen stupiden allgemeinen Code, der den Computer immer wieder die Matrizenmultiplikation durchführen lässt. Das ist unnötig viel Herumgerechne für den Computer, spart uns aber langweilige Rechnerei. Und vor die Wahl gestellt, selber einmal öde Rechnungen zu machen oder sie die den Computer wieder und wieder durchführen zu lassen, fällt die Antwort natürlich leicht: Der Computer soll lieber immer und immer wieder unnötig rechnen! Gucken wir also schnell noch mal in den Wikipedia-Artikel Matrix (Mathematik) um nachzugucken, wie man zwei Matrizen miteinander multipliziert und schreiben wir uns die Matrizenklasse in unserem lineare Algebra-Paket:
public class Matrix {
// Die Elemente einer 3x3-Matrix
private double[][] elements;
// Erzeugt eine leere Matrix
public Matrix(){
this.elements = new double[3][3];
}
// Erzeugt eine 3x3-Matrix durch explizite Angabe aller 9 Elemente
public Matrix(double A11,double A12,double A13,double A21,
double A22,double A23,double A31,double A32,double A33){
this.elements = new double[3][3];
this.elements[0][0] = A11;
this.elements[0][1] = A12;
this.elements[0][2] = A13;
this.elements[1][0] = A21;
this.elements[1][1] = A22;
this.elements[1][2] = A23;
this.elements[2][0] = A31;
this.elements[2][1] = A32;
this.elements[2][2] = A33;
}
// Gibt das i,j-te Element der Matrix aus
public double getElement(int i, int j){
return this.elements[i-1][j-1];
}
// Multipliziert zwei 3x3-Matrizen (einfach mal stupide ausgeschrieben)
public static Matrix multiply(Matrix A, Matrix B){
double c11 = A.getElement(1,1) * B.getElement(1,1) +
A.getElement(1,2) * B.getElement(2,1) +
A.getElement(1,3) * B.getElement(3,1);
double c21 = A.getElement(2,1) * B.getElement(1,1) +
A.getElement(2,2) * B.getElement(2,1) +
A.getElement(2,3) * B.getElement(3,1);
double c31 = A.getElement(3,1) * B.getElement(1,1) +
A.getElement(3,2) * B.getElement(2,1) +
A.getElement(3,3) * B.getElement(3,1);
double c12 = A.getElement(1,1) * B.getElement(1,2) +
A.getElement(1,2) * B.getElement(2,2) +
A.getElement(1,3) * B.getElement(3,2);
double c22 = A.getElement(2,1) * B.getElement(1,2) +
A.getElement(2,2) * B.getElement(2,2) +
A.getElement(2,3) * B.getElement(3,2);
double c32 = A.getElement(3,1) * B.getElement(1,2) +
A.getElement(3,2) * B.getElement(2,2) +
A.getElement(3,3) * B.getElement(3,2);
double c13 = A.getElement(1,1) * B.getElement(1,3) +
A.getElement(1,2) * B.getElement(2,3) +
A.getElement(1,3) * B.getElement(3,3);
double c23 = A.getElement(2,1) * B.getElement(1,3) +
A.getElement(2,2) * B.getElement(2,3) +
A.getElement(2,3) * B.getElement(3,3);
double c33 = A.getElement(3,1) * B.getElement(1,3) +
A.getElement(3,2) * B.getElement(2,3) +
A.getElement(3,3) * B.getElement(3,3);
Matrix C = new Matrix(c11,c12,c13,c21,c22,c23,c31,c32,c33);
return C;
}
// Multipliziert einen Vektor mit einer Matrix
public static Vector multiply(Matrix A, Vector X){
double x1 = A.getElement(1,1) * X.getX() +
A.getElement(1,2) * X.getY() +
A.getElement(1,3) * X.getZ();
double x2 = A.getElement(2,1) * X.getX() +
A.getElement(2,2) * X.getY() +
A.getElement(2,3) * X.getZ();
double x3 = A.getElement(3,1) * X.getX() +
A.getElement(3,2) * X.getY() +
A.getElement(3,3) * X.getZ();
return new Vector(x1,x2,x3);
}
}
So. Die Drehmatrizen um die verschiedenen Koordinatenachsen können wir uns, vielleicht im Paket "Koordinatentransformationen", auch schon mal vorbereiten:
/*
* Gibt eine Drehmatrix aus, die um einen Winkel "angle" (im Bogenmaß) dreht,
* und zwar wahlweise um die x-Achse (dimension = 1), y-Achse (dimension = 2)
* oder z-Achse (dimension = 3)
*/
public static Matrix getRotationMatrix(int dimension, double angle){
Matrix rot = new Matrix();
switch(dimension){
// Drehung um die x-Achse
case 1: rot.setElement(1, 1, 1.0);
rot.setElement(2, 2, Math.cos(angle));
rot.setElement(3, 3, Math.cos(angle));
rot.setElement(3, 2, Math.sin(angle));
rot.setElement(2, 3, -1.0 * Math.sin(angle));
break;
// Drehung um die y-Achse
case 2: rot.setElement(2, 2, 1.0);
rot.setElement(1, 1, Math.cos(angle));
rot.setElement(3, 3, Math.cos(angle));
rot.setElement(1, 3, Math.sin(angle));
rot.setElement(3, 1, -1.0 * Math.sin(angle));
break;
// Drehung um die z-Achse
case 3: rot.setElement(3, 3, 1.0);
rot.setElement(1, 1, Math.cos(angle));
rot.setElement(2, 2, Math.cos(angle));
rot.setElement(2, 1, Math.sin(angle));
rot.setElement(1, 2, -1.0 * Math.sin(angle));
break;
}
return rot;
}
}
Wir sind schon so gut wie am Ziel! Alles zusammen verwenden wir in einer letzten Methode, die in der Klasse "Keplersche Umlaufbahn" den Ortsvektor des Planeten ausrechnet:
/*
* Berechnet die Position des Planeten zu einer Zeit t in kartesischen,
* von der Bahn des Planeten unabhängigen Koordinaten
*/
public Vector getPositionInSpace(JulianDate t){
// Im ersten Schritt gerechnen wir die Position in der Bahnebene des Planeten in
// Kugelkoordinaten:
Vector polar = getPositionInOrbit(t);
// Jetzt wandeln wir von Kugelkoordinaten in kartesische Koordinaten um:
Vector cart = CoordinateTransformations.sphericalToCartesian(polar);
/* Jetzt müssen wir von einem kartesischen Koordinatensystem in der Bahnebene
so drehen, dass wir den Vektor in einem für alle Planeten gemeinsamen
Koordinatensystem haben.
Erst machen wir uns die benötigten Drehmatrizen: */
// Kippt die Bahnebene relativ zur Bezugsebene, d.h. der Ekliptik:
Matrix rotateI = CoordinateTransformations.getRotationMatrix(1,this.i);
// Dreht die Knotenlinie:
Matrix rotateOMEGA = CoordinateTransformations.getRotationMatrix(3,this.OMEGA);
// Dreht zum sonnennächsten Punkt der Bahn:
Matrix rotateOmega = CoordinateTransformations.getRotationMatrix(3,this.omega);
// Die Gesamtdrehmatrix ist dann das Produkt der einzelnen Drehmatrizen:
Matrix rotation = Matrix.multiply(Matrix.multiply(rotateOmega,rotateI),rotateOMEGA);
// Führe die Drehung aus:
return Matrix.multiply(rotation, cart);
}
Am Ziel!
Mit ein paar einfachen Zeilen können wir uns jetzt die uns interessierenden Größen berechnen. Z.B. so:
public static void main(String[] args) {
// Erzeuge die Erdumlaufbahn:
KeplerianOrbit ErdOrbit = new KeplerianOrbit(Planet.EARTH);
// Erzeuge die Venusumlaufbahn:
KeplerianOrbit VenusOrbit = new KeplerianOrbit(Planet.VENUS);
// Wähle ein beliebiges Datum, z.B. den 27.1.2012, um 23:30 und 30 Sekunden:
JulianDate T = new JulianDate(27, 1, 2012, 23, 30.5);
// Berechne die Position der Erde im Raum zu diesem Zeitpunkt:
Vector positionErde = ErdOrbit.getPositionInSpace(T);
// Berechne die Position der Venus im Raum zu diesem Zeitpunkt:
Vector positionVenus = VenusOrbit.getPositionInSpace(T);
// Schreibe den Abstand der Erde zur Sonne aus:
System.out.println("Abstand Erde - Sonne: " +
Vector.norm(positionErde) + " AE");
// Schreibe den Abstand der Venus zur Sonne aus:
System.out.println("Abstand Venus - Sonne: " +
Vector.norm(positionVenus) + " AE");
// Schreibe den Abstand zwischen Erde und Venus aus:
System.out.println("Abstand Erde - Venus: " +
Vector.norm(Vector.subtract(positionErde, positionVenus)) + " AE");
}
Dann lesen wir auf dem Bildschirm:
Abstand Erde - Sonne: 0.98472761878588 AE
Abstand Venus - Sonne: 0.7229524281728524 AE
Abstand Erde - Venus: 1.1308756929560395 AE
Problem gelöst. Fertig. Jetzt haben wir ein kleines Spielzeug in der Hand, mit dem man lauter lustige Sachen machen könnte. Aber wir wollen nur einen kurzen Blick darauf werfen, wie unsere Berechnungen so aussehen.
Wie es aussieht
Die berechneten räumlichen Positionen der Planeten könnten wir zum Beispiel benutzen, um das Aussehen des Sonnensystems zu bestimmten Zeiten graphisch darzustellen . So könnten wir uns etwa die Umlaufbahnen der Planeten ausrechnen lassen und die Positionen der Planeten, z.B. einfach mal für den kommenden Sonntag, mittags um 13:31 MEZ. Blickt man von Norden auf die Ebene der Erdbahn, dann sieht das innere Sonnensystem mit den Planeten Merkur, Venus, Erde und Mars dann so aus:
 |
| Das innere Sonnensystem am 10. März 2013, um 13:31 MEZ, gesehen von nördlich der Ekliptik. (Zur Orientierung: Der Frühlingspunkt ist rechts, die Planeten laufen gegen den Uhrzeigersinn). |
Beliebige andere Blickwinkel gehen natürlich auch. Gehen wir einfach mal in die Bahnebene der Erde und gucken uns das Sonnensystem "von der Seite" an:
 |
| Derselbe Zeitpunkt, aber gesehen aus Richtung des Früh- lingspunkts, von innerhalb der Ekliptik (Man beachte, daß die Z-Achse gegenüber der Y-Achse stark überhöht ist!). |
 |
| Nochmal dasselbe, aber diesmal wenn der Beobachter sich gegen- über der vorherigen Abbildung um 90 Grad gegen den Uhrzeigersinn in der Ekliptik weiterbewegt. |
Wie gut sind wir?
Wie genau sind denn jetzt unsere Berechnungen mit dem "Wikipedia-Sonnensystem", verglichen mit der Realität? Sind unsere Ergebnisse glaubwürdig, oder was? Als Referenz nehmen wir mal das HORIZONS-System des JPL. Hey, das ist die NASA! Wenn die nicht weiß wie's wirklich ist, wer denn dann?? Mit diesem System (es hat natürlich auch einen Wikipedia-Artikel!) können wir uns Größen, die wir mit unserem kleinen Code berechnen, ebenfalls berechnen (zu den gleichen Zeitpunkten, versteht sich) und die Genauigkeit unserer Ergebnisse so überprüfen. Als Vergleichsgrößen nehmen wir uns mal den innersten Planeten, Merkur, und den äußersten, Neptun, sowie die Erde. Wir rechnen jeweils in 30-Tage-Schritten die Abstände dieser Planeten zur Sonne sowie die Abstände von Merkur und Neptun zur Erde aus und bestimmen die Abweichung zum Referenzwert aus HORIZONS. Dabei gehen wir mal so grob 100 Jahre in die Vergangenheit und die Zukunft und berechnen die Fehler vom 1.1.1900 bis ins Jahr 2105. Für die Abstände zur Sonne sehen die Fehler dann so aus: |
| Der relative Fehler im Abstand Planet - Sonne. Die Punkte haben einen Abstand von 30 Tagen im Zeitraum 1900 - 2105. Schwarz: Merkur Blau: Erde, Rot: Neptun. |
Gehen wir zu Neptun, d.h. zu den roten Punkten. Das sieht schon schlimmer aus. Und es sieht falsch aus. Und es ist falsch. Da ist einmal ein kleines Gewobbel. Aber da ist auch eine große, nach einer "Schwingung" aussehende Abweichung. Wobei, "groß" ist immer noch unter einem Prozent. Aber es sieht nach einem systematischen Fehler aus. Vielleicht sind die Bahnelemente in der Wikipedia nicht so gut? Und tatsächlich stimmen die aus der Wikipedia entnommenen Bahnelemente für alle Planeten einigermaßen mit denen überein, die man sonst wo auch in der Literatur finden kann, ausgenommen eben Neptun. Für den finden wir in anderen Quellen, z.B. hier, merklich andere Werte, insbesondere für die mittlere Anomalie. Wenn wir statt der Wikipedia-Bahnelemente diese anderen benutzen, verschwindet die große Abweichung:
 |
| Dasselbe wie vorher, aber mit korrigierten Bahnelementen für Neptun. |
Dann bleibt da noch der Merkur. Für den werden die Fehler tendentiell immer größer, je weiter man sich vom Referenzzeitpunkt, dem 1. Januar 2000, entfernt. Hier scheinen tatsächlich deutliche Störungen der Umlaufbahn siechtbar zu sein. Und Störungen, die zu Abweichungen von einer idealen Keplerbahn führen, werden in unserem Vorgehen überhaupt nicht berücksichtigt. Aber auch hier ist der Fehler unter einem Prozent über einem Zeitraum von +/- 100 Jahren.
Für die Abstände sieht es natürlich ganz ähnlich aus. Da die Erdbahn ziemlich genau gerechnet wird, steigen die Fehler nur wenig an. Korrigiert man die Bahnelemente des Neptun, so ist der Abstand zwischen ihm und der Erde sehr gut bestimmt und für Merkur liegt der Fehler bei ca. 1% über einen Zeitraum von 200 Jahren.
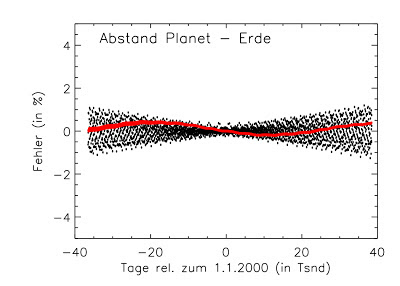 |
| Der relative Fehler im Abstand Planet - Erde. Schwarz: Merkur Rot: Neptun. |
Und das sind ja Genauigkeiten, mit denen man so für den Hausgebrauch, etwa wenn man sich mal sein Horoskop selber ausrechnen will, ganz gut leben kann.
 |
| Dasselbe nochmal, aber mit korrigierten Bahnelementen für Neptun. |
Fazit
Unter dem Strich bleibt also: Die Wikipedia bietet alles, was man zur Berechnung der Positionen der Planeten braucht. Und das nicht nur irgendwie im Prinzip, sondern auch für die ganz praktische Durchführung. Dabei liegt der Fehler unter einem Prozent über den Zeitraum von 1900 bis 2100, oft sogar deutlich unter einem Prozent.Die größte Begrenzung der Genauigkeit ist bei unserem Versuch hier, daß Bahnstörungen, etwa durch die Gravitationswirkung der Planeten untereinander, nicht berücksichtigt wurden. Dabei wäre es gar nicht besonders schwierig, sie in das Java-Projekt einzubauen! Am einfachsten lassen sie sich näherungsweise integrieren, indem man die Bahnelemente nicht, wie hier, als für alle Zeiten konstant annimmt, sondern sie selber als Funktionen der Zeit auffasst. Die Einflüsse der Planeten untereinander lassen dann die Bahnelemente mit der Zeit langsam driften. Oft reicht es schon, einen kleinen, in der Zeit linearen Term zu den Bahnelementen zu addieren, und schon steigt die Genauigkeit deutlich. Man muß nur zu jedem Julianischen Datum nicht die Standardbahnelemente zum Zeitpunkt 1.1.2000 benutzen, sondern die jeweils aktuellen Bahnelemente in einem Zwischenschritt ausrechnen. Viel komplizierter würden unsere Rechnungen nicht, und daß es so geht, deutet sie Wikipedia auch hier und da an. Allerdings fehlen konkrete Angaben, wie schnell die einzelnen Bahnelemente der Planeten driften. Und wir wollten ja nur Informationen aus der Wikipedia benutzen. Aber daß ja auch das tolle an der Wikipedia: Irgendwann wird irgendwer diese Zahlen nachtragen, und dann kann man noch eine Stufe besser werden mit seinem Wikipedia-Sonnensystem!
So, und jetzt kommen wohl noch diejenigen, die behaupten, im Internet gäbe es doch eh nur Schmutz und Schund und Pöbeleien und Gemobbe! Da gucka, hä? Komm her und isch fick deinen Brockhaus, Alta!
Also um deine These aus dem ersten Absatz zu beweisen solltest du vllt eher (kontroverse) politische Themen o.ä. nehmen wo auch diverse Leute ein Interesse an einer Verfälschung haben. :P
AntwortenLöschenNaja, wo findet man schon völlig unverfälschte Informationen zu kontroversen politischen Themen? Zeitungen, Schulbücher, Blogs, Armutsberichte,... überall findet man politisch motivierte Einfärbungen, da finde ich vollkommene Objektivität auch von einem Lexikon etwas viel verlangt...
LöschenSchick. Ist das der Grundstock der Doktorarbeit, die Du neulich erwähnt hast?
AntwortenLöschen:D
LöschenIch will beweisen, daß, was die Geisteswissenschaften können, in den Naturwissenschaften erst recht klappt!
Und da hat die NASA Hunderte hochbezahlter Spezialisten, um die Flugbahn ihrer Shuttles zu berechnen, wo sie das doch einfach irgendeinen Nerd aus der IT aus Wikipedia abkupfern lassen könnten. Die werden sich ärgern, dass sie jahrzehntelang derart viel Geld unnütz verbrannt haben...
LöschenWaren doch bloß Steuergelder. Hätte man die nicht schon an die Spezialisten rausgehauen, würden die jetzt eh in irgendeine Bankenrettung oder militärische Invasion gehen!
Löschen..mein Sohn möchte gerne wissen, wie Ameisen und Marienkäfer pinkeln und wie Ameisenkacke aus sieht.
AntwortenLöschenStatt die Wikipedia zu durchforsten hab ich es mir einfach gemacht und einen Biologen gefragt.
Was für spannende Fragen! Aber immer wenn man einen Biologen braucht, ist keiner da. Und überhaupt, lernt man im Biologiestudium, wie Ameisenkacke aussieht? Also, ich bin mir nicht sicher, ob ich einem Biologen da einfach so glauben würde! :)
Löschen..der Biologe findet die Fragen toll und hat sich eine Woche Nachforschungszeit erbeten
Löschen:D
Ich bin doch tatsächlich hier gelandet, indem ich "fick deinen brockhaus" gegoogelt hab...
AntwortenLöschenHa! Das heißt, DWüdW hat wieder einmal einen exotischen Suchbegriff für sich belegt! Schade nur, daß so wenige Leute sich für das Ficken von Brockhäusern interessieren...
LöschenIch möchte mich ausdrücklich dagegen verwahren, einfach von jedem dahergesurften Internetkasper gefickt zu werden!
LöschenWas zickst' denn so rum, kannst' doch 'n Dirndl ausfüllen! Vielleicht sogar zwei.
LöschenNö, für Dirndl bin ich zu kantig, das wäre nichts.
LöschenMit welcher Software machen Sie diese schönen Diagramme?
AntwortenLöschenMit IDL.
Löschen